Часто эксперты автомобильных изданий, рассказывая о выдающейся динамике машины, в первую очередь превозносит огромный крутящий момент двигателя, оставляя мощности роль второго плана. Мол, благодаря именно моменту машина ровно и напористо разгоняется в широком диапазоне оборотов и скоростей. Особенно востребовано это качество на высших передачах, – ведь тяговые силы и ускорения на них в любом случае не столь велики, как на первой или второй передаче. А для безаварийного движения в потоке транспорта возможность быстро прибавить скорость зачастую играет судьбоносную роль. Ездить на таком автомобиле даже психологически легче. И все же, когда нужно быстрей разогнаться, что важней – мощность или крутящий момент?
Сразу отметим: чаще всего эти два параметра «конфликтуют»… в головах журналистов, охотно повторяющих признанные публикой «истины» без какого-либо их анализа. На самом же деле смешно рассматривать мощность в отрыве от крутящего момента и наоборот. Первая показывает энергию, ежесекундно вырабатываемую двигателем, тогда как крутящий момент – всего лишь силовой фактор, показывающий, как нагружен при работе коленчатый вал. Крутящий момент может существовать и сам по себе, без мощности. Например, при неожиданной остановке перегруженного двигателя на крутом подъеме, в песке, при буксировке тяжелого прицепа в какой-то миг момент еще есть, а движения уже нет. А в некоторых механизмах можно обнаружить и длительно действующий на какой-нибудь вал момент, удерживающий его от поворота. Например, в рулевом механизме, когда мы лишь удерживаем управляемые колеса в нужных положениях, тогда как дорога пытается их нарушить. А самый типичный пример: пытаясь открутить «прикипевший» болт, ключ удлинили метровой трубой, – а болт ни с места. Момент огромный, а работа не идет. А коли нет работы – то нет и мощности.
Мощность момент 0.jpg
Тут впору вспомнить школьную физику. Нарисуйте круг радиуса R – это будет сечение вала – и приложите к нему «касательную» силу F. Крутящий момент этой силы М = F • R. За один оборот вала сила F пройдет путь 2R – и выполнит работу: А = F • R • 2 = М • 2. А работа за n оборотов: А = М • 2 • n. Если n – число оборотов в минуту, то работа за одну секунду – то есть, мощность – составит N = М • 2n /60.
Выражение 2 n /60 = 0,1047 n = – угловая скорость вала. Итак, N = М • 0,1047 n (Формула [1]).
Но мы имеем дело не только с вращающимися деталями, но и движущимися линейно. В этом случае в формуле (1) момент М заменим силой F, а угловую скорость – линейной v. Получим: N = F • v (Формула [2]).
Эти формулы равноправны. Замерив, например, тяговую силу колес, умножим на достигнутую машиной скорость – и найдем затрачиваемую мощность. Но если крутящий момент на ведущей оси умножить на угловую скорость колес, получим то же самое.
Итак, мощность – это работа (или энергия) израсходованная или произведенная за 1 секунду. Конечно, о «законе сохранения энергии» знает каждый. Говоря по пионерски, она «не возникает из ничего», но и не исчезает, не оставив следа. Так, лишь около четверти тепловой энергии, получаемой двигателем от сгорания топлива, превращается в механическую, соответствующая мощность (эффективная) тратится на движение машины. Большая же часть полученной в цилиндрах двигателя теплоты идет на «обогрев» окружающего нас мира.
Эффективная мощность тоже доходит до ведущих колес не вся – до 15 % ее может рассеять в виде тепла трение в узлах и агрегатах трансмиссии. Но для нас важней другое: если при открытом дросселе (или при полной подаче топлива в дизель) двигатель выдает на колеса сколько-то киловатт, то это – его «потолок». Никакими простыми механизмами вроде коробок передач, редукторов и т. п. превысить эту величину невозможно – этого «закон сохранения» не допустит.
Итак, крутящий момент – это удобный для нас «инструмент», связывающий процессы в двигателе с трансмиссией машины и ведущими колесами. Но не более того! Ракетчики, например, запрягают пламя напрямую, получают гигантские тяги и мощности, но о крутящих моментах вспоминают лишь в расчетах турбонасосных агрегатов, – да и то, если двигатели не твердотопливные!
Из формулы (1) видно, что для получения достаточной мощности вовсе не обязателен огромный крутящий момент, ведь в произведении два сомножителя. Почему бы, например, не увеличивать мощность при постоянном моменте, наращивая угловую скорость в каком-то диапазоне оборотов? При этом мощность растет по оборотам линейно. А постоянство момента в заданном диапазоне – не чудо, которым некоторые почему-то восторгаются, а всего лишь признак постоянства тяговых сил. Если пренебречь сопротивлением воздуха (к примеру, на первой передаче оно невелико), то и ускорение машины в этом диапазоне постоянное. Это довольно удобно для водителя. Но спросим себя: если бы в начале диапазона момент был таким же, а ближе к пресловутым «верхам» стал больше, стал бы с таким «подхватом» автомобиль хуже? – Вряд ли. Разве только что-нибудь нарушилось бы в смысле экологии.
Мощность можно менять и при постоянных оборотах. Пример: мы ехали со скоростью 90 км/ч по горизонтальному шоссе, а с началом подъема, дабы сохранить скорость, пришлось больше открыть дроссель. Это увеличение момента в чистом виде.
Итак, имеем дело с формулой (1). К примеру, перед нами скромный двигатель грузовика с моментом 35 кгм при оборотах 3000 в минуту. Какова мощность? Тут отметим, что в расчетах всегда важен правильный выбор единиц измерений параметров. Угловую скорость измеряют в 1/сек. А момент? – В старых единицах это кгм. Получаем: N = 35 кгм . 0,1047 . 3000 1/сек = 10993 кгм/сек 146,6 л.с. А в современной системе СИ: 35 кгм = 343,35 Нм. Тогда N = 343,45 Нм • 0,1047 • 3000 1/сек 107846 Вт.
На всякий случай напомним, что 1 лс = 75 кгм/сек = 75 • 9,81 Нм/сек = 735,75 Вт. Поэтому 107846 Вт 146,6 л.с.
А теперь прикинем мощность «формульного» двигателя с таким же скромным моментом, но при оборотах 18 тысяч! Результат – 880 л.с. (647 кВт), которые обеспечивают машине роскошную динамику. Никакого чуда нет: чем больше циклов совершит наш «моментик» за одну секунду, тем больше и совершенная им работа. Еще пример. В авиатехнике ныне практически господствуют газотрубинные двигатели. Повторив наш расчет для небольшого двигателя, с оборотами свободной турбины 40 тысяч в минуту, получим мощность около 1950 л.с. или 1438 кВт. Момент турбины невелик, но ведь воздушный винт приводится от нее не напрямую, а через редуктор, – а уж «мощи» ему хватает!
Но вернемся к автомобилю. Как уже сказано, любому комфортней ездить на машине, у которой под капотом достаточно и мощности, и момента. Но многим приходится ездить на скромных авто, возможности коих, как нынче говорят, «очень бюджетные»! Всякий, кто не умеет вовремя переключать передачи, с ними испытывает неприятности. Значит, надо учиться, друзья. Ну а что делать владельцу авто с АКП? На смену недовольству двигателем зачастую приходят претензии к автомату. Нередко – справедливые, ведь у АКПП тоже случаются специфические болячки, требующие ремонта. Но часто они оказываются не обоснованными: современный автомобиль, насыщенный электроникой и настроенный изготовителем на строгое выполнение жестких экологических норм, вовсе не обязан подстраиваться под любую российскую лихость!
Гусеничному трактору дернуться и оборвать сцепку – плевое дело. Это похоже на выстрел из ружья – можно на миг и «формулу I» опередить. А дольше – никак. Ружье от ракеты отличается принципиально: последняя сохраняет нужное ускорение достаточно долго. В свое время, при стартах к Луне гигант «Сатурн 5» массой свыше 3100 т отделялся от пускового устройства мягко, как пассажирский поезд, – с ускорением чуть больше 1 м/сек2. А минут через пять, по мере выгорания топлива, настолько «терял в весе», что его скорость перед выключением первой ступени составляла 3 км/сек.
Низшая передача бульдозера крайне «коротка»: чуть «перекрутил» – тяга упала. А другие не лучше, – вон и «формула» уже растворилась за горизонтом, так что для серьезных игрищ «мощи» на гусеницах маловато.
Если пренебречь разницей в КПД передач (она невелика), то на любой передаче машину движут одни и те же киловатты. Но движут по-разному. Момент и тяговая сила на ведущих колесах подчиняются «золотому правилу»: сколько процентов выиграешь в скорости, столько потеряешь в силе. Это показывают рис. 1 и 2. Если двигатель заведомо слаб, с ним сильно не разгонишься.
Мощность момент 1.jpg
Рис. 1. Величины мощности N1 ... N5 на ведущей оси не зависят от включенной передачи. Точки пересечения кривой Nсопр с кривыми N3, N4 и N5 дают информацию о максимальных скоростях автомобиля на этих передачах. Здесь самая скоростная на горизонтальной дороге в безветрие – четвертая.
Вся история современной транспортной техники – это непрерывная борьба за большие мощности. У наиболее знаменитых ракетоносителей они давно превысили 100 миллионов кВт. Это не ошибка - именно 100 000 000 000 Вт, или 100 ГигаВатт. И хотя притязания автомобилиста не столь велики, «прохватить» на динамичной машине всякий не прочь.
Главные враги любителя скорости – не гаишники, а силы, тормозящие движение, – от этих не откупишься! Мощность сопротивления воздуха вкупе с мощностью шинных потерь показаны на рис. 1 линией Nсопр.
(Желающие посчитать, могут воспользоваться следующими формулами. Nсопр. = Nw + Nf. Мощность аэродинамических потерь Nw для автомобиля весом 15000 Н при плотности воздуха 1,25 кг/м3, Сх = 0,3 и лобовой площади S = 2 • м2 составляет: Nw = (0,3 • 2 • 1,25)/2 • v3 = 0,375 v3 Вт. А мощность шинных потерь Nf = 0,015 • 15000 • v = 225 v Вт. При 100 км/ч Nсопр составляет лишь 14,5 кВт. А при 200 км/ч – 77 кВт. Разница впечатляет?)
Колеса автомобиля, борясь с мощностями сил сопротивления, при максимальной скорости полностью расходуют мощность, получаемую от двигателя. Но ее характеристика (например, показанная кривой N4 на рис.1) при полностью открытом дросселе похожа на гору с округлой макушкой, тогда как характеристика мощности сопротивлений Nсопр. поднимается как крутая парабола. Чтобы полностью использовать арсенал мощности двигателя – и получить максимум скорости V4 (на горизонтальной трассе, без ветра), передаточное число трансмиссии и размер шин подбирают так, чтобы кривая Nсопр пересекла кривую N4 возле вершины. Максимальные скорости на третьей и пятой передачах (V3 и V5) существенно ниже. Но на спуске или с ветром вдогон выгодней может стать пятая передача, а на подъеме или с ветром в лоб – третья.
Другие враги скорости – подъем дороги и встречный ветер. Подъем с углом всего 1,5% добавит к потерям в шинах еще столько же. Но еще коварней ветер. Его скорость сложится со скоростью машины относительно дороги, – и уже эту сумму в расчете затрат мощности надо возвести в куб! При скорости по спидометру 36 км/ч (10 м/сек) и ровном встречном ветре 5 м/сек мощность Nсопр вырастет лишь на 0,9 кВт, а вот при 180 км/ч (50 м/сек) – аж на 15,5 кВт. Но придуманный нами автомобиль так ехать не может… Маловато мощи! Максимальная скорость снизится почти на 20 км/ч.
Мощность момент 2.jpg
Рис. 2 - Так зависит крутящий момент (М1….М5) или тяговая сила (Fтяг 1 …Fтяг 5) на ведущей оси от включенной передачи. При коэффициенте сцепления шин с дорогой 0,7 ведущая ось, нагруженная половиной веса машины (Gавтом = 15000 н), может создать реальную тяговую силу не больше Fмакс. доп. = 5250 Н.
На рис.2 величины крутящего момента М1…М5, а заодно и теоретические тяговые силы F1…F5 на ведущей оси, показаны одними и теми же кривыми, – ведь тяговые силы пропорциональны моментам. Величины сил – на вертикальной оси справа. Но тут важно учесть следующее.
Разгоняет машину не вся тяговая сила, а лишь избыточная – то есть разница между полной тяговой силой колес и сопротивлением воздуха. Отношение этой силы к весу машины академик Чудаков назвал динамическим фактором D. На первой передаче сопротивление воздуха мало, его можно не учитывать – считать, что машину разгоняет полная сила Fтяг.1. Но отталкиваться от дороги сильней, чем позволяет сцепление шин, невозможно! Если, например, ведущая ось несет половину веса машины – 7500 Н, то при коэффициенте сцепления = 0,7 тяговая сила не может превысить 35% ее веса. Это неплохо согласуется с такой официальной характеристикой любого автомобиля как предельно возможный угол подъема. С «моноприводом» трудно получить больше. Правда, у машины с задним приводом на подъемах ведущие колеса несколько догружаются весом машины, а вот передний тут невыгоден. Лучшая схема, но сложная и дорогая, – полный привод (конечно, не с такой скромной мощностью, как у «Нивы» или УАЗа!).
Если избыточная сила (на первой передаче, например) слишком велика, машина «шлифует» дорогу. Дело нелепое, нужно перейти на следующую передачу. А вот при разработке нового авто конструктор учитывает высокую мощность двигателя и ее следствие – тяговые силы в передаточных числах трансмиссии. Передачи проектируются как достаточно «длинные», расширяющие диапазон скоростей при достаточных ускорениях. А это значит, что и при более высоких скоростях действуют нужные тяговые силы (или моменты) на колесах. Иначе говоря, реализуется весь арсенал мощности! Значит, она все же важнее.
Споры на тему влияния мощности-момента ведутся давно, и конца им не видно. Вроде бы сто раз уже объясняли самыми разными способами, что тут к чему, а воз и ныне там. Вызывает неподдельный интерес, откуда все же берется заблуждение и почему оно такое устойчивое?
Причин видится две. Одна из них в том, что мощность есть функция от момента. Зависимость мощности от момента стоит барьером, который преодолеть оказывается непросто. Что странно. Поскольку очевидность того, что мощность есть функция не только от момента, но и от оборотов, не оспаривается, и тот факт, что у разных двигателей бывает весьма большой разброс по соотношению мощности к моменту, также не подвергается сомнению. То есть существует молчаливое согласие с тем, что мощность есть функция от двух аргументов - оборотов и момента, но при этом зависимость от оборотов как бы игнорируется. Почему?
А в этом и есть вторая, главная причина заблуждения. И ключевая фраза здесь: "Человек совершенно может не иметь понятие про мощность.А вот разницу в ускорении на 3 и 4 передаче он вполне способен почувствовать." Ясно, что на динамику автомобиля оказывают большое влияние и передаточные числа КПП. На графике 1 видны кривые мощности двигателя, смещенные в зависимости от разных передаточных чисел и кривая сопротивлений. Видно, что с ростом передаточного числа динамика резко возрастает. Это очевидно и вопросов не вызывает. Странно, что не менее очевидный факт, что бОльшая часть времени при разгоне приходится вовсе не на 1 и 2 передачи, а на 3-4, при этом упускается из виду.
При разгоне здравомыслящий водитель пользуется всеми четырьмя передачами и весьма широким диапазоном частот вращения двигателя. При этом редко задумывается о том, что динамика разгона на высокой скорости мала и плохо ощущается, но именно на нее и приходится львиная доля времени разгона (по той простой причине, повторю, что на высших передачах динамика хуже и потому занимает больше времени). Хорошо ощущается динамика разгона на низших передачах, в диапазоне низких и средних оборотов (дальше водитель двигатель раскручивает редко). И что выходит? А выходит, что "низовой", моментный двигатель дает ощущение уверенного и бодрого разгона по той простой причине, что легко и весело страгивает и начинает разгонять автомобиль. А по достижении скорости ощущения становятся слабыми, и оценить разницу в разгоне 100- и 120 сильного моторов на 4-5 передачах, способен не каждый. Потому и кажется, что момент определяет динамику. По ощущениям. А ощущениям человек склонен верить очень сильно, даже вопреки логике и здравому смыслу.
Проповедующие формулировку "скорость определяется мощностью, а динамика разгона - моментом двигателя" могут убедиться в своем заблуждении, решив простую задачу.
Вводные
1. Равномерный подъем на некоторую высоту равносилен равномерному ускорению, поскольку увеличивает потенциальную энергию тела mgh*. (что можно объяснить - чем с большей высоты упадет, тем сильней ударится).
2. Поднимаем равномерно груз весом 75 кг на высоту 1 м за 1 с.
3. Имеется черный ящик, в котором спрятан мотор неизвестной природы и, возможно, редуктор с КПД=1.
Вопросы.
1. Какая мощность должна быть в моторе, спрятанном внутри черного ящика?
2. Какой момент должен быть в моторе, спрятанном внутри черного ящика?
Подъем указанного груз на нужную высоту за время аналогичен разгону по горизонтали той же массы с ускорением g0.5.
Если ускорение определяется моментом - просто назовите цифру
Если ускорение определяется мощностью - тоже просто назовите цифру
Если цифру назвать не удается, значит параметр может быть самым разным и роли не играет.
Вы можете разгонять тело с заданным ускорением (или поднимать его вверх), меняя крутящий момент по своей прихоти (и устанавливая каждый раз соответствующий редуктор). Вы можете отталкиваться от параметров редуктора, и всякий раз требуемый момент будет меняться и зависеть от передаточного отношения этого редуктора. Но всегда мощность будет оставаться одной и той же, неизменной величиной - для подъема груза 75 кг на 1 м за 1с понадобится ровно одна лошадиная сила или 0,73549875 кВт
Можно поступить и следующим образом.
Берите любой момент, который причина разгона, берите любой редуктор и разгоните тело 75 кг до скорости 3.13 м/c за 1 с.
Ограничение только по мощности - она не должна превышать 0.9 л.с.
Есть ли решение у этой задачи? Если нет - то почему?
Ответ.
Задача не имеет решения по той простой причине, потому что невозможно обеспечить заданную динамику - для нее не хватит мощности. Каким бы ни был момент.
Вывод. Момент двигателя для разгонной динамики не имеет значения, все решает мощность.
* Пояснение Вы поднимаете 75 кг получаете от этого энергию mgh. Она преобразуется так:
поскольку a = V2 / 2h, а ускорение а у нас равно g, то V = (2hg)0.5.
Кинетическая энергия тела E = mV2/2 = m2hg/2 = mgh.
x


 Курилка раздела Ford Mondeo
Курилка раздела Ford Mondeo 



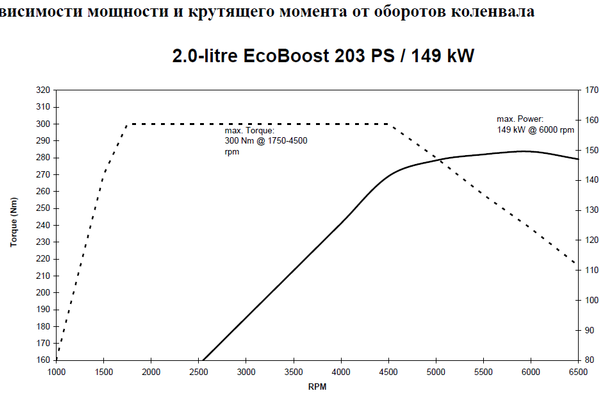
 при бодром движении по городу 15-17л/100 на экобусте, это к баапке гадалке не ходи
при бодром движении по городу 15-17л/100 на экобусте, это к баапке гадалке не ходи 
 сам при покупке мечтал о 2,2, но не сложилось
сам при покупке мечтал о 2,2, но не сложилось

 а это как минимум на 200-250 т.р. дороже, а экобуст 240 вообще был без проблем.. бери не хочу
а это как минимум на 200-250 т.р. дороже, а экобуст 240 вообще был без проблем.. бери не хочу  ан нет, ездят на равных
ан нет, ездят на равных 

 5 Apr
5 Apr



 Dark mode
Dark mode