Есть на форуме математики?

Nebelius
Мда... полная каша
К примеру, как ты определил координату "х" красной точки? Это ж все даже не проекция чего-то трехмерного на плоскость, а просто рисунок чего-то трехмерного на плоском листе бумаги. Размеры по оси Х на рисунке не соответствуют реальным... А как твои красные точки в пространстве соотносятся с заданными в задаче на плоскости?... Кроме того, измерения линейкой может на практике и помогают, но вот в задачах геометрии на построение чего-то (а не рисование) не канают.

Salavat
При произвольном положении трех точек заданные лучи только по чистой случайности могут оказаться биссектрисами искомого треугольника.

- Красный -:

Salavat При произвольном положении трех точек заданные лучи только по чистой случайности могут оказаться биссектрисами искомого треугольника.

да я уж понял... поэтому и написал - не про то я

- Красный -:

Nebelius Мда... полная каша К примеру, как ты определил координату "х" красной точки? Это ж все даже не проекция чего-то трехмерного на плоскость, а просто рисунок чего-то трехмерного на плоском листе бумаги. Размеры по оси Х на рисунке не соответствуют реальным... А как твои красные точки в пространстве соотносятся с заданными в задаче на плоскости?... Кроме того, измерения линейкой может на практике и помогают, но вот в задачах геометрии на построение чего-то (а не рисование) не канают.

Вроде понятно объяснил.

Строю проекцию точки на две оси. (красная линия) беру линейку меряю расстояние от 0 до проекции записываю.
Все 3 точки имеют только 2 координаты , третья = 0.

По найденому уравнению плоскости подставляя (X, 0, 0) (0, Y, 0) (0,0 Z) нахожу точки пересечения плоскости с осями. Отмеряю линейкой опять же и ставлю эти точки.

Данное решение кончено не геометрическое а алгебраическое. Но это всё равно решение

Надо геометрическим решением буду думать дальше.

- Красный -
Я подумал только седня.
Через точку (1) можно провести множество прямых, через две точки - тока одну (на ней будет лежать одна сторона треугольника).
У нас есть одна точка (1), нужно найти ей вторую (А), которая будет являться вершиной треугольника. Но (А) и (1) будут на второй стороне треугольника.
Т.о. делаем вывод, что решение одно. Осталось его найти , час потратил - пока ниче.

VRTM
Мыслишь правильно, но пока нет идеи... Обрати внимание на пост Зомбе. Хотя кто знает, может найдешь другой вариант решения. Мне было бы интересно, т.к. знаю только один вариант.

- Красный -
судя по посту Зомбе, надо искать построение пересечения с пирамидой в Начертательной геометрии.
хотябы здесь - http://lib.ru/TEXTBOOKS/GEOMETRY/gordon.txt

Salavat
Начертательная геометрия тут вовсе не обязательна. Достаточно с помощью пространственного рисунка представить себе построение плоскости и её пересечения с пирамидой, и все построения ортогонально спроецировать на плоскость рисунка. Тогда на рисунке появятся проекции тех линий, которые рисуются в пространстве. Т.е. "выезд" в пространство это как бы вспомагательная штука, которая является обоснованием проведения тех линий, которые мы будем рисовать на плоскости рисунка... их в принципе можно нарисовать и без воображаемой пирамиды, но тогда будет непонятно, почему мы рисуем именно такие линии и почему они пересекутся именно на заданных лучах.

- Красный -

На лучах ставим 3 точки это будет основание пирамиды ... (точки ставим заведомо дальше углов нашего треугольника для простоты)

Дальше стоим объемную пирамиду по проекции (расположение основания и вершины пирамиды в 3Д берем от балды чтоб проще рисовать было)

После строим наши известные точки на пирамиде рисуем прямую проходящую через центр лучей, нашу точку и заканчивающуюся на грани основания пирамиды (всё это делаем на проекции) потом переносим точку на основании пирамиды на объемную фигуру, а следом постоив прямую на гране пирамиды строим нашу известную точку.

После этого остается только найти пересечение двух плоскостей (грань пирамиды (А) и плоскость образованная нашими 3 точками (Б)). Делаем это через секущую плоскость. Точки персечения это плоскости с А и с Б отображаем на проекцию. получится 4 точки (а1, а2) и (б1, б2) из них получаем 2 прямые, которые персекаються в одной точке. Эту точку перносим на объемный рисунок она должна быть на нашей секущей плоскости. Теперь строим прямую персечения А и Б соеденив новую точку и одну из известных точек на этой грани. Пересечение новой прямой с углом грани пирамиды даст нам один из углов искомого треугольника.

- Красный -
в Начерталке, просто всё это по-шагам расписано - как строить

Nebelius
Salavat
Сорри, уже сильно тороплюсь на дачу, вечерком в воскресенье отвечу... Ваше здоровье

Мне кажется я достаточно четко описал решение? Или мне просто кажется?

AlexZombie
Согласен ...
Я расписал твое решение по шагам ...

Но думаю у Красного есть более простое решение ... есть подозрение что пирамида по проекции строится так чтобы нужная плоскость не отображалась.

Nebelius
От того, как ты выберешь три точки будет зависить наклон ребер пирамиды, да и неоднозначно это все. Думаю, не вариант.
AlexZombie
Имхо, тут трехмеркой не должно пахнуть. Я на работе думал с этим уклоном, но сам себя не убедил никак. Думаю, если без всего можно "на глаз" найти решение на плоскости, то должно быть элементарное графическое построение.
Последняя мысль была - зависимость между углами, но её тоже нет .

VRTM
да - в Начерталке всё это расписано

Чисто интуитивно, развивая идею зависимости между углами:
- дано: черный цвет
- строим сначала коридор (параллельны тому лучу, который между линиями) из красных линий
- и строим сторону треугольника (зеленая), которая гипотетически перпендикулярна биссектрисе полученного угла
- остальные стороны отобразил пунктиром

В ПН в Автокаде надо проверить теорию. Доказать тоже пока не могу (вечер же )

VRTM
перебор - неудачный.
нужен следующий вариант.

я после 3-го (такого не пробовал) - забил.
Вобщем: написано на люке бака мин95 - лью 95 и 98. Написано в данном случае - в Начерталке

VRTM:

Nebelius От того, как ты выберешь три точки будет зависить наклон ребер пирамиды, да и неоднозначно это все. Думаю, не вариант.

В том то и прикол что от выбора точек основания пирамиды ничего не зависит ... мы же имеем дело с проекцией пирамиды на плоскость ...

Упрощенное решение, чтобы "на пальцах".

Берем этот рисунок.
Представляем, что линии это растяжимые нити, резинки. А три наших точки нарисованы на стекле, которое может пропускать через себя эти самые нити. Приподнимаем стекло с точками к себе. Теперь зажимаем пальцами центральную точку пересечения прямых и тащим её к себе. Поднимаем вершину другим словом. Проекция не меняется, все нормально. Поднимаем эту точку до тех пор, пока точки не лягут на стороны пирамиды.

Так вот плоскость стекла, которая рассечет пирамиду в итоге даст нам один единственно возможный треугольник.

AlexZombie
never use drugs

- Красный -, оказывается вариант Nebelius единственный, который работает.

На оси прямоугольной системы координат можно посмотреть повсякому, в т.ч. как и в твоей задаче.
Т.е. имеем систему координат и три точки. осталось найти пересечение.

Т.е. в данной задаче предполагаем, что лучи и точки - это проекции системы координат и точек на нашу произвольную "рабочую плоскость".

VRTM
вообще былобы неплохо - доказать (через а=б, АБВ=ГДЕ,...)

VRTM
Мы немного о разных вещах говорим. Я привожу доказательство, что этот треугольник существует и он один. Построить моим способом на бумаге не получится.

Salavat

Оси системы координат есть. Точки есть. Как проекции точек построить уж не объясняю.
Кстати, ваще грубо ступил выше - много лишнего нарисовал. Исправляюсь:
Условно обзовем оси SХ, SY, SZ.
В общем, плоскость "123" нужно пересечь плоскостью "1bc" параллельной "XSY", но проходязей через точку "1".
Естественно, будет и пересечение с отрезком "23" в точке "а" (желтые построения).
Т.к. "1bc" параллельна "XSZ", то и их линии пересечения с "123" будут параллельны. Поэтому через точку "2" строим прямую, параллельную "1а", это и будет сторона искомого треугольника.
AlexZombie
Да, то что один треугольник я понимаю . Просто изначально думал, что в плоскости тоже решение будет. Да и до сих пор думаю, что оно есть - только прячется

VRTM
Твоё решение проще и покрасивше того что предложил AlexZombie и потом расписал я через начерталку.

Тока в описании ошибка:

цитата:

Т.к. "1bc" параллельна "XSY",

"1bc" параллельна "XSZ" в твоих обозначениях.

Плюс надо добавить что точки 1, 2, 3 принадлежат плоскостям XSY, YSZ, ZSX соотв.

AlexZombie
Как построить твоим способом на бумаге я вроде детально расписал. Конечно не очень просто но возможно.

А доказательство что такой теругольник есть и он всего дин есть и в решении VRTM

Muk

по ходу хитрый Зомбе всем рассказывал про Париж, а сам втихую смотал в Амстер

baraNEO
Не пали

VRTM

цитата:

В общем, плоскость "123" нужно пересечь плоскостью "1bc" параллельной "XSY", но проходязей через точку "1".

Если точка "a" принадлежит прямой "23", то "ас" не параллельна "1b"... а если прямая "ac"параллельна "1b", то у неё нет пересечения с прямой "23"... см. рисунок под катом, надеюсь там понятно... Над самой идеей покумекаю, но в любом случае должна быть процедура отображения воображаемых построений в пространстве на плоскость исходной задачи... Пока её не улавливаю.

В общем, я решал задачу так...
1. На плоскости задачи строим произвольный треугольник с вершинами на заданных лучах так, чтобы заданные точки попали внутрь этого треугольника. Очевидно, это можно сделать при любом положении точек. Назовем его для удобства - большой треугольник.
2. Представим себе, что получившаяся картинка есть ни что иное, как ортогональная проекция треугольной пирамиды на плоскость задачи. Точка "О" это ортогональная проекция вершины пирамиды, заданные лучи это ортогональная проекция рёбер пирамиды, большой треугольник это основание пирамиды, а заданные точки это ортогональная проекция соответствующих точек, расположенных на гранях пирамиды (см. Рисунок 1).

3. Дальнейшая идея состоит в следующем... Если мы построим пересечение плоскости А1В1С1 с гранями (а значит и с рёбрами) большой пирамиды, то ортогональная проекция этого пересечения на плоскость задачи даст нам искомый треугольник...
4. Ортогональная проекция всех построений в пространстве на плоскость исходной задачи приведена на Рисунке 2... Рисовать построения в пространстве и их ортогональные проекции уж больно хлопотно. Поэтому все построения приведены на плоскости исходной задачи, при этом не сложно представить себе, проекцией каких построений в пространстве они являются.

На рисунке 2 большой черный треугольник это основание большой пирамиды. Черные точки это те самые заданные точки. 1,2 и 3 это заданные лучи, которые в рамках наших представлений являются ортогональной проекцией рёбер большой пирамиды на плоскость исходной задачи. Центральная черная точка (обозначим её буквой О... некуда было впиндюрить это обозначение на рисунке) это ортогональная проекция вершины О1 большой пирамиды. Последовательность построений следующая...
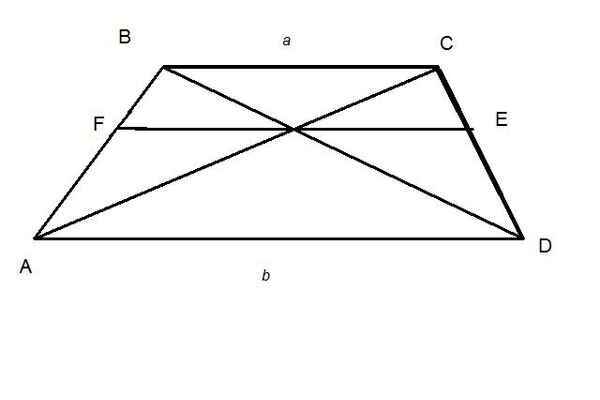
4.1. Через точку О и заданные черные точки проводим три луча до пересечения со сторонами большого черного треугольника. Получаем зеленые точки А, В и С, образующие зеленый треугольник АВС. Представьте себе, что зеленый треугольник это основание маленькой треугольной пирамиды. Тогда ОА, ОВ и ОС это ортогональная проекция рёбер малой пирамиды на плоскость исходной задачи, а черные (заданные в исходной задаче) точки расположены на рёбрах этой маленькой пирамиды.
Возьмем две черные точки на грани О1АВ и проведем через них линию до пересечения с продолжением стороны АВ маленькой пирамиды. В результате получим точку "b", которая обладает следующими свойствами - она одновременно принадлежит плоскости боковой грани маленькой пирамиды, плоскости исходной задачи и, что важно, принадлежит плоскости трех точек на гранях большой пирамиды. Аналогично, берем две точки на на рёбрах грани О1АС маленькой пирамиды и строим точку "a". Прямая "ab" является пересечением "плоскости трех точек на гранях большой пирамиды" с плоскостью основания обоих пирамид. А точка пересечения "d" этой прямой с продолжением основания большой пирамиды принадлежит одновременно боковой грани большой пирамиды и "плоскости трех точек на гранях большой пирамиды". Вторая точка, обладающей теми же свойствами (на той же грани большой пирамиды) нам дана в виде проекции на плоскость пирамид. Соединяя их прямой (красной), получаем проекцию пересечения плоскости боковой грани большой пирамиды с "плоскостью трех точек на гранях большой пирамиды", т.е. то, что и искали. Пересечение красной прямой с лучами 1 и 2 даёт две красные точки искомого в задаче треугольника. Дальше очевидным образом получаем третью точку красного треугольника на луче 3.

- Красный -:

VRTM цитата: В общем, плоскость "123" нужно пересечь плоскостью "1bc" параллельной "XSY", но проходязей через точку "1". Если точка "a" принадлежит прямой "23", то "ас" не параллельна "1b"... а если прямая "ac"параллельна "1b", то у неё нет пересечения с прямой "23"... см. рисунок под катом, надеюсь там понятно... Над самой идеей покумекаю, Скрытый текст x

Там походу ошибка в построении ...

Надо было бы соединить точку 3 с точкой проекцией точки 2 на плоскость YSZ 'это будет проекция прямой 2-3. Пустить прямую из точки Б параллельную оси Z до проекции прямой 23. От этой точки прямая до пересечения с прямой 23 параллельно очи Х.
Полученная прямая АС || 1Б.

Это плоскость параллельная XSZ. Сотв. прямая 1А параллельная прямой проходящей через точку 2.

цитата:

но в любом случае должна быть процедура отображения воображаемых построений в пространстве на плоскость исходной задачи... Пока её не улавливаю.

то что мы видим и есть отображение воображаемых построений на плоскость экрана ...

Nebelius

цитата:

Надо было бы соединить точку 3 с точкой проекцией точки 2 на плоскость YSZ 'это будет проекция прямой 2-3. Пустить прямую из точки Б параллельную оси Z до проекции прямой 23. От этой точки прямая до пересечения с прямой 23 параллельно очи Х. Полученная прямая АС || 1Б. Это плоскость параллельная XSZ. Сотв. прямая 1А параллельная прямой проходящей через точку 2.

Опять не получится... Если красная точка (см. рис. по катом) это проекция 2 на плоскость YSZ, то плоскость "23красная точка" не параллельна плоскости XSY. Поэтому, пуская параллель от нового положения точки "c" не пересечемся с прямой 23... пройдем мимо неё, получатся не пересекающиеся скрещенные прямые. Точку "a" на прямой 23 так не получишь.

цитата:

то что мы видим и есть отображение воображаемых построений на плоскость экрана ...

Тогда получается так... Есть некая ортогональная система координат. Ортогональная проекция осей этой системы координат на плоскость задачи есть заданные лучи. Получаем ту же пирамиду, что и у меня... координатные квадранты это грани пирамиды, а сама пирамида опирается на плоскость исходной задачи своей вершиной.