Надо срочно решить...до утра...Могу сыну проиграть МНОГО...

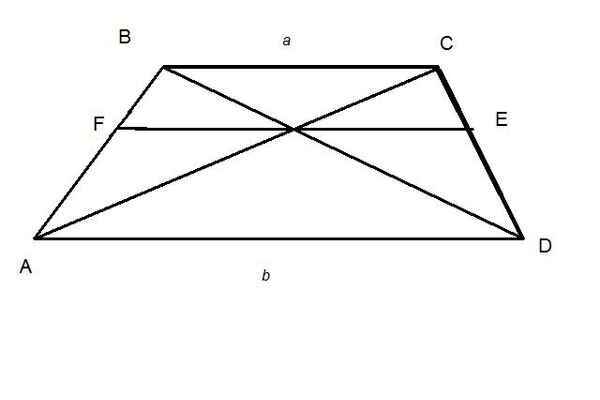
Условия:Есть трапеция...Есть диагонали трапеции...Через точку пересечения диагоналей параллельно основаниям трапеции проведен отрезок, концы которого находятся на боковых сторонах трапеции.Известны размеры оснований:
а и
b.Необходимо найти длину отрезка
EF...Необходимо РЕШЕНИЕ, т.к. ответ знаю:
2ab/(a+b ) Помогайте...
З.Ы. Мне так кажеться, что решения надо искать через подобия треугольников...
Блин...до чего форум довел...не могу решить задачу за 8 класс...

Олегин
10 February 2009
Есть на форуме математики?
- Красный -:
|
Кстате, пространственное воображение и оптическая иллюзия это все-таки разные вещи. 
|
соглашусь на сто процентов, просто новую тему открывать не хотелось, а без знания математики и геометрии, такую иллюзию не посторить (я свое видео к первому посту вынес)
Швым:
|
- Красный -
вот те и геометрия
лучшая иллюзия на мой взгляд |

это - стереометрия (или как там называют объёмною). Геометрия - это на плоскости.
- Красный -
Раз 0.3 не верно, то 0.1. Т.к. в пирамиду вообще маленький квадрат влезет. А если еще считать какой объем от шариков он замерет, то цифра будет еще меньше.
- Красный -Методом исключения остается 0.5, хмм...чо реально с прицелом проблемы чтоли

Для тех, кого интересуют формулы по первой задаче:
1. Высота правильного тетраэдра с ребром а: а*sqrt(6)/3
2. Высота правильной пирамиды: а/sqrt(2)
Т.о. высота рисунка слева: 2*50*sqrt(6)/3+2*25
справа: 2*50/sqrt(2)+2*25
т.к. 1/sqrt(2)<sqrt(6)/3, то левая пирамида выше

- Красный -
14 October 2010
VRTM:
|
- Красный -
Методом исключения остается 0.5, хмм...чо реально с прицелом проблемы чтоли  |
0,5 это примерно для такой укладки
Тут в уме можно посчитать - шар радиуса R в кубе со стороной 2*R. Отношение равно пи делить на 6, что примерно равно 0,52. Для ромбоэдрической укладки (так называется укладка, как в треугольной пирамиде), очевидно должно быть больше. Подсказка - один из отвечавших попал, а я слукавил, сказав, что промазал.

NicklasМолодец, но не применимо для задачи, у шариков ребер нет. И реальная высота пирамиды из шариков будет меньше, чем по формуле.
- Красный -| цитата: |
| Чему будет равно отношение объема шаров к объему кубика |
Хотя если имеется в виду объем куба и объем "вырезанных" (до этого я думал объем всех шариков к объему вырезанных кубиком шариков) шариков таким кубом, то >0.3. Даже на глаз бы тоже ошибся и утверждал 0.7.
Смутило в условии наличие пирамидки

- Красный -
14 October 2010
VRTMКстати, если интересно... Есть, казалось бы, плоская задачка, но решается методом "выезда" в пространство (ну, по крайней мере, я другого решения не знаю). Формулируется так - есть три луча на плоскости и три точки. Надо построить треугольник так, чтобы его вершины находились на лучах, а заданные точки - на его сторонах.
Скрытый текстЭто, правда, самобоян, но если интересно, не ищи - покумекай сам.

x
- Красный -
14 October 2010
Чо, опять загрузил на весь день... писец работе?

- Красный -
Ну судя по всему надо представить что 3 луча это оси координат 3 мерного пространства
Все три точки лежат на 3 плоскостях образованных двумя осями. Рассчитываем координаты точек и по координатам получаем уравнение плоскости проходящей через эти точки. из уравнения получаем координаты пересечения плоскости с осями ...
Как-то так.
Ну если лучи на плоскости и точки на плоскости, то думаю легко. Методом научного тыка займет минут пять, однако, как построить аргементированно - подумаю
- Красный -
14 October 2010
Nebelius
Нет... ты неправильно понял намек на "выезд" в пространство. В данном случае лучи и точки находятся в одной плоскости. А вот, что такое "выезд" в пространство, это надо сообразить.
VRTM
Ну, не мне тебе рассказывать, что такое геометрическое построение... там понятие научного тыка отсутствует.
- Красный -
14 October 2010
Petrovich71Если нет доказательной процедуры построения, то нет гарантии, что твои стороны тр-ка "встретятся" на заданных лучах. Построение "на глаз" в геометрии не канает.

- Красный -
14 October 2010
1
Petrovich71:
|
- Красный -
Мамай клянусь в паинте строил!  |
Тада уж в КорелДро нуно было... а чтоб все выглядело тип-топ, нуно было нарисовать треугольник, а потом на его сторонах точки поставить. Тогда бы все выглядело натуральнее.

- Красный -:
|
VRTM
Кстати, если интересно... Есть, казалось бы, плоская задачка, но решается методом "выезда" в пространство (ну, по крайней мере, я другого решения не знаю). Формулируется так - есть три луча на плоскости и три точки. Надо построить треугольник так, чтобы его вершины находились на лучах, а заданные точки - на его сторонах.
Скрытый текстЭто, правда, самобоян, но если интересно, не ищи - покумекай сам.  x |
Самое первое, что в голову приходит - представить, что это не лучи в одной плоскости, а трехмерная сетка координат так нарисована - сразу понятно становится
- Красный -
Щас нарисую решение как его вижу я ... то что всё лежит на плоскости отнють не означает что эти оси нельзя представить в 3D.
AlexZombie
 15 October 2010
15 October 2010
Nebelius
Да все элементарно. Представляем лучи проекциями и строим по проекциям пирамиду. Рассекаем пирамиду плоскостью, проходящей через три точки (она одна-единственная). Проекция этого сечения даст треугольник.
вот нашел
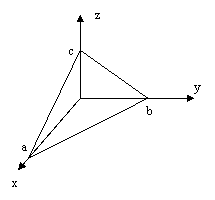
Убираем прямые которые мы ищем и ставим на них точки которые даны ... и вуаля наши исходные данные задачи ... (оси x, y, z совсем не обязаетльно должны быть под 90град.)
- Красный -
15 October 2010
AlexZombieВспомнил мою задачку из своей темы про Смекалку или сам догадался? Кстати, там изложена только идея решения. А как в итоге будет выглядеть проекция построения на плоскости?

- Красный -
15 October 2010
Nebelius| цитата: |
| Убираем прямые которые мы ищем и ставим на них точки которые даны ... |
Еси чесно, ничё нипонял

... переведи

Прямых (сторон тр-ка), которые мы ищем на рисунке нет... Как можно убрать то, чего нет???

... а потом еще и точки на них поставить?
Nebelius
 15 October 2010
15 October 2010
1
- Красный -Вот добавил красные точки.
Прямы ab-bc-ca это то что мы ищем.
Оси это замена твоих лучей ... ессно они могут быть произвольными ...
- Красный -:
|
VRTM
Кстати, если интересно... Есть, казалось бы, плоская задачка, но решается методом "выезда" в пространство (ну, по крайней мере, я другого решения не знаю). Формулируется так - есть три луча на плоскости и три точки. Надо построить треугольник так, чтобы его вершины находились на лучах, а заданные точки - на его сторонах.
Скрытый текстЭто, правда, самобоян, но если интересно, не ищи - покумекай сам.  x |
в ВУЗе помню было, точно

. спецом - есть пункт в общей программе.
Вот только предмет уже не помню - Начертательная геометрия, кажется.
ещё вариант (но - слабее) - Стереометрия.
решение - уже не помню на память,..
- Красный -
15 October 2010
Nebelius
Хорошо... пусть лучи это координатные оси... есть три точки. Как построить, а не нарисовать прямые ab, ac и cd? Как известно любая прямая однозначно задается двумя точками... По одной точке на искомых сторонах тр-ка задано. Чтобы построить (а не нарисовать) любую сторону тр-ка нужно найти еще одну точку на этой стороне кроме красной... А точка в геометрии однозначно задается как пересечение двух прямых или кривых. К примеру, как ты определил положение точки "a"? Одна прямая задана, это заданный луч. А где заданная (а не искомая) другая прямая (или кривая)?
- Красный -:
|
Nebelius
К примеру, как ты определил положение точки "a"? Одна прямая задана, это заданный луч. А где заданная (а не искомая) другая прямая (или кривая)? |

Построил проекции на оси (красные линии) взял линейку и замерил ... воткнул цифры сюда
http://www.webmath.ru/web/prog9_1.php
из уравнения получил пересечения плоскости с осями ... опять же линейкой отмерил и поставил точку

Хотя согласен решение далеко не самое точное

но для некоторых вариантов можно получить приемлимый вариант ...
удалил. не про то вроде я






 это - стереометрия (или как там называют объёмною). Геометрия - это на плоскости.
это - стереометрия (или как там называют объёмною). Геометрия - это на плоскости.





 14 Oct
14 Oct






 ... переведи
... переведи  ... а потом еще и точки на них поставить?
... а потом еще и точки на них поставить?


 Dark mode
Dark mode